認識神經網路
神經元(Neuron)
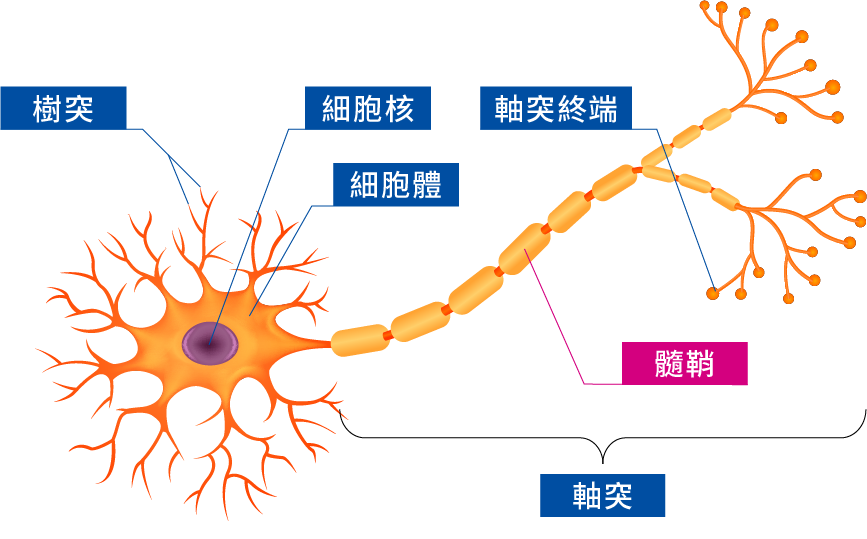
構造
- 細胞本體:控管整個神經元。
- 樹突:輸入。
- 神經纖維:傳遞訊息,如果越常使用,此神經會的反應會越明顯。
- 軸突:輸出。
運作方式
感知器(Perceptron)
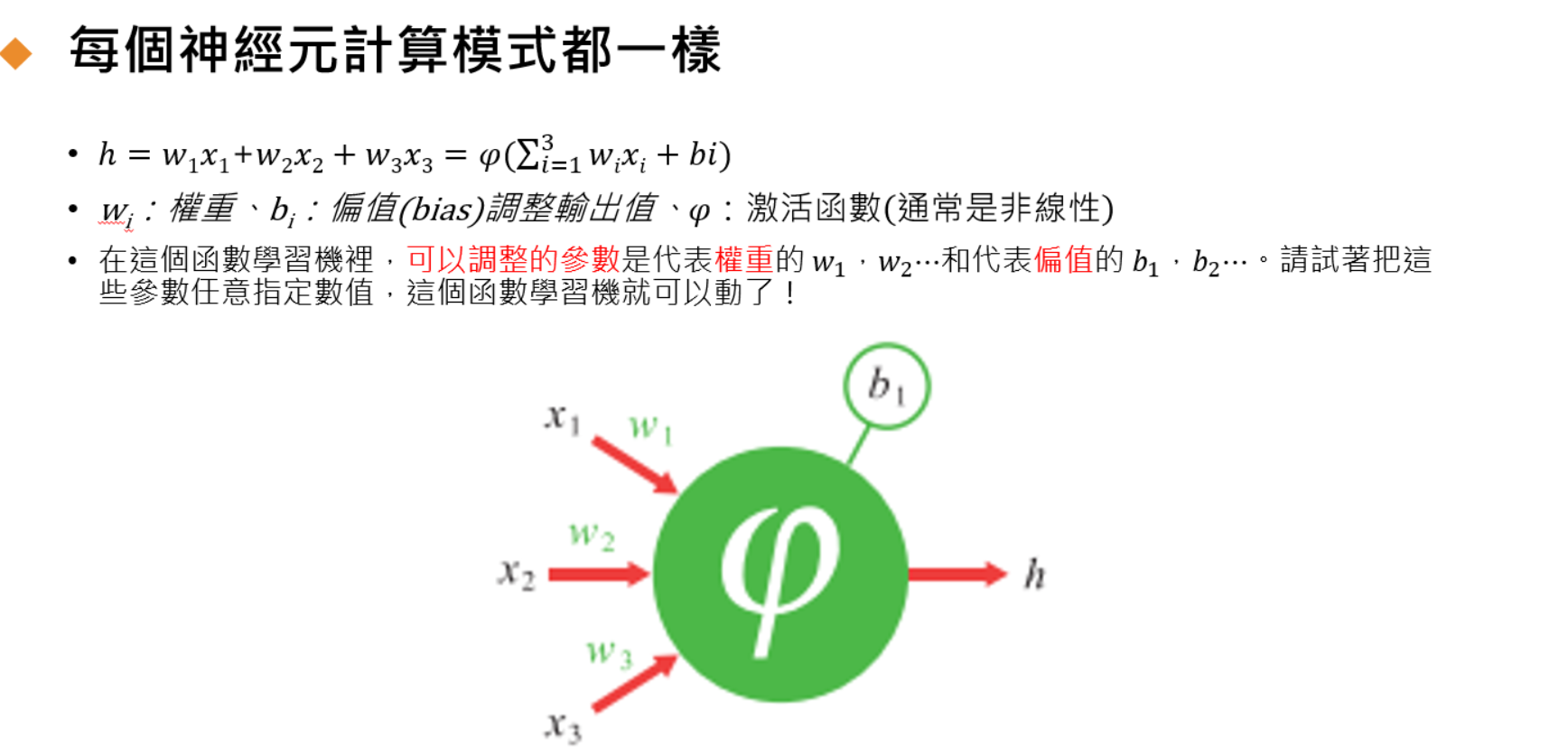
構造
- x:輸入數值。
- w:權重,代表輸入數值的重要程度,正如神經纖維的反應會變動一樣,這表示權重的數值會不斷的改變,這也是為甚麼AI模型需要經過不斷的訓練。
- φ:激勵函數,規範數值的範圍
- b:偏移,加權總和要超過甚麼數字才有意義,用以規範數值有意義的範圍。
- h:輸出數值,也就是所獲得的結果。
以圖像來思考,綠色為正的權重,紅色為負的權重,顏色愈亮代表與0的差距越大。神經元透過權重來計算下一層神經元所注重的圖像。而我們可以將我們所要的圖像外的權重值都改為0。如果想要確認圖形的邊,可以在外圍的偏移改為負的權重,就可以得到最大的加權總和。
什麼是邏輯函數(Sigmoid Function),這個函數有什麼特別之處?
我們想要計算權重的總和,加權總和可能為任意實數,但我們需要將加權總和壓縮在0到1之間(不包含0且不包含1)以便利用,sigmoid function(邏輯函數)就是使加權總和壓縮在0到1之間的工具,如圖。
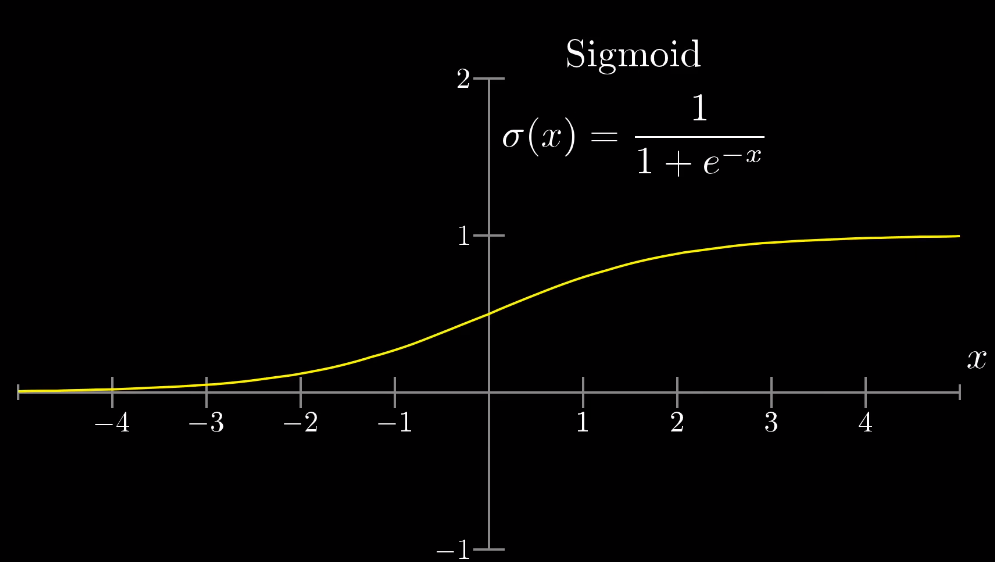
眼尖的人應該有發現,方程式內的稱為激勵函數,而下文介紹的是邏輯函數,事實上,邏輯函數只是激勵函數的一種,激勵函數還有ReLU、tanh、Maxout函數等等,範圍也不僅限於0或1之間,不過那是另一個故事了
那到底為甚麼要套入激勵函數呢,因為如果不這麼做,會導致方程式為線性函數,那為甚麼會是線性函數呢?以國中數學舉例來說,f(x) = 2x +1,g(x) = 3f(x) + 2,則f(x)帶入後會得到g(x) = 3(2x+1) +1,g(x)= 6x+4,還是一個線性函數。
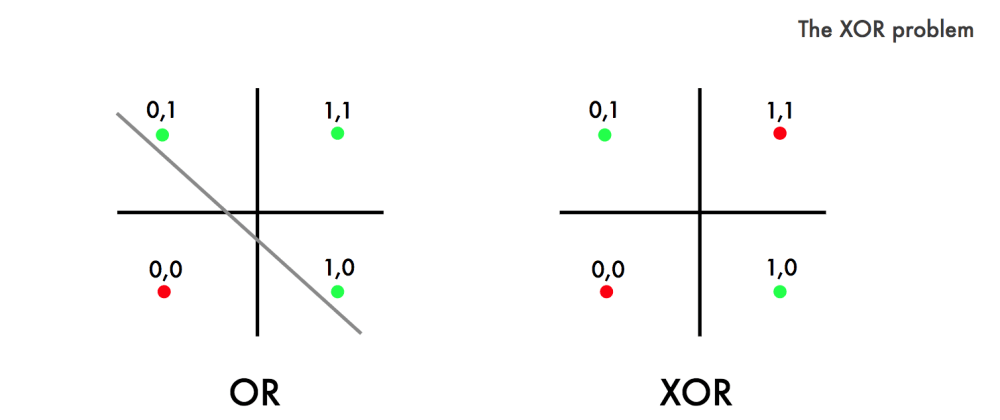
這代表你只要給了每個輸出都獨立對一個輸出,一開始就是因為沒有加上這個邏輯函數導致原函數是線性的,這個線性函數解決不了exclusive or的問題。
如圖,一條線是無法分開綠色的點與紅色的點的。這也導致連結主義學派沒落好一段時間……
多層感知機
運作方式
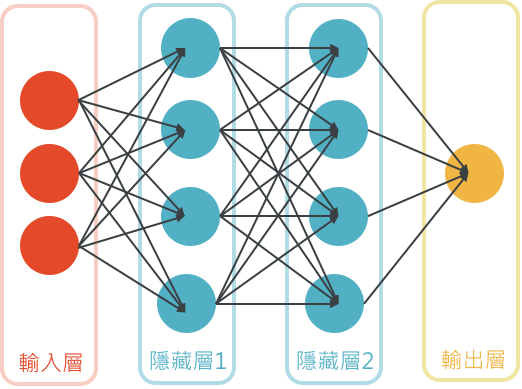
多層感知機是一種前向傳遞類神經網路,還有一點要注意的是隱藏層並不是越多越好。
也有反向傳遞的方式,在損失函數調整偏值後,會重新調整先前所有權重的值,用來降低誤差
其餘更詳細歡迎看:機器學習-神經網路-多層感知機
資料來源:
About this Post
此文章由 IHCT 所撰寫,版權聲明:CC BY-NC 4.0.